Illustration de l’impact du coût de l’effet de levier sur les rendements
Il y a quelques semaines, j’ai présenté un billet de blog intitulé Volatilité de l’ère Trump : l’impact sur les allocations de portefeuille, dans lequel je soulignais que l’augmentation de la volatilité a généralement pour effet de réduire les allocations optimales de portefeuille au profit d’allocations plus sûres.
Il s’agissait d’un de ces articles où l’on se dit d’abord «Eh bien, c’est évident», mais où l’on apprécie le fait que j’ai «prouvé» l’intuition à l’aide d’illustrations. Bien que la volatilité des marchés ait été incroyablement faible depuis lors, j’ai du mal à imaginer que cela puisse durer. Cela ressemble un peu à une réaction de «cerf dans les phares» de la part des investisseurs, car le train Trump se met en marche si rapidement qu’ils ne peuvent que tirer les rideaux.
Je pense qu’à un moment donné, à moins que le Donald ne devienne soudainement un président banal, nous verrons ces allocations changer.
Mais il y a quelques jours, j’ai eu une autre prise de conscience qui m’a fait penser aux mêmes vieux graphiques CFA-Level-I. J’expliquais à quelqu’un qui voulait que je lui parle de la façon dont les entreprises sont gérées. J’expliquais à quelqu’un qui voulait que je tire parti de notre stratégie de suivi de l’inflation* vraiment géniale que tirer parti d’un rendement à un chiffre est très logique lorsque le coût de l’effet de levier est nul, mais pas tant que cela lorsque le coût de l’effet de levier est à un chiffre. J’en ai déjà parlé – en octobre 2023
j’ai publié «L’impact de la hausse des taux sur les stratégies à effet de levier», j’ai montré un tableau, mais il existe un moyen très simple d’illustrer la même chose.
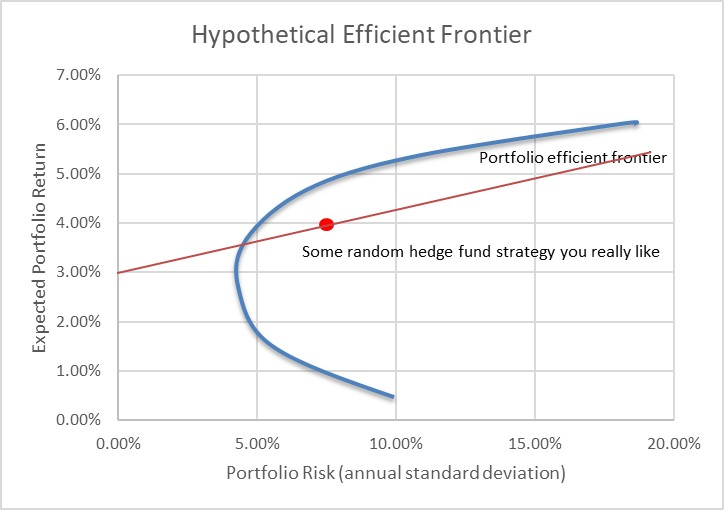Frontière efficiente hypothétique
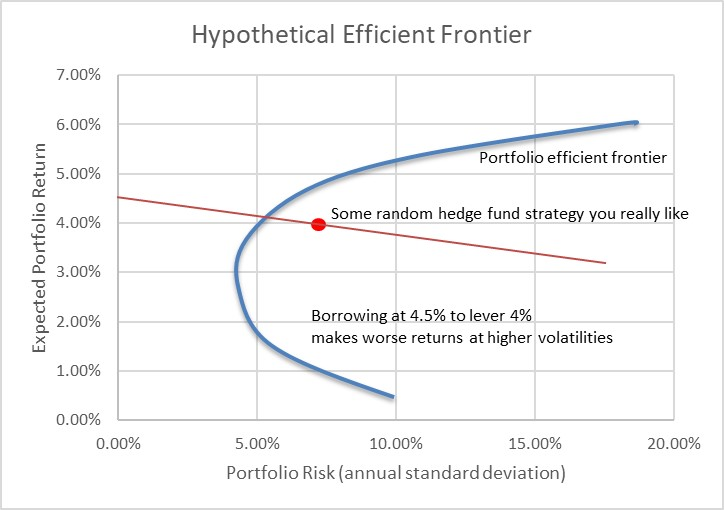
Je n’ai pas vraiment besoin de la frontière efficiente du portefeuille ici. Peut-être que l’optimiseur produit une part du portefeuille optimal qui représente un investissement dans une stratégie de fonds spéculatif que vous aimez vraiment. Peut-être que ce n’est pas le cas. Plus probablement, vous n’utilisez même pas d’optimiseur.
Mais si vous aimez vraiment cette stratégie, mais que vous souhaitez des rendements plus élevés, vous demandez au gestionnaire : «Hé, pouvez-vous faire un effet de levier ?
Le gestionnaire répond par l’affirmative. Mais il ne peut pas vous donner deux fois plus de rendement pour deux fois plus de risque – le calcul de l’effet de levier ne fonctionne pas de cette manière. Si le coût de l’effet de levier est de 3 % – ce qui est le cas dans ce graphique car c’est là que la ligne touche l’axe, à un taux sans risque de 3 % – alors votre rendement pour deux fois le risque est de (2 x 4 % – 1 x 3 %) = 5 %. Vous n’obtenez donc qu’un rendement de 1 % pour un risque doublé.
Vous pouvez le voir sur le graphique car c’est le point que traverse la ligne rouge : 5% de rendement, 15% de risque. Pour un risque multiplié par trois, vous obtenez (3 x 4 % – 2 x 3 %) = 6 %. Et ainsi de suite. La pente de la ligne est telle que 7,5 % de risque supplémentaire vous donne 1 % de rendement supplémentaire, quel que soit le nombre de fois que vous utilisez l’effet de levier.
Alors pourquoi les gens demandent-ils un effet de levier ? Parce que depuis 2008, le taux d’intérêt au jour le jour était généralement de 0 %.
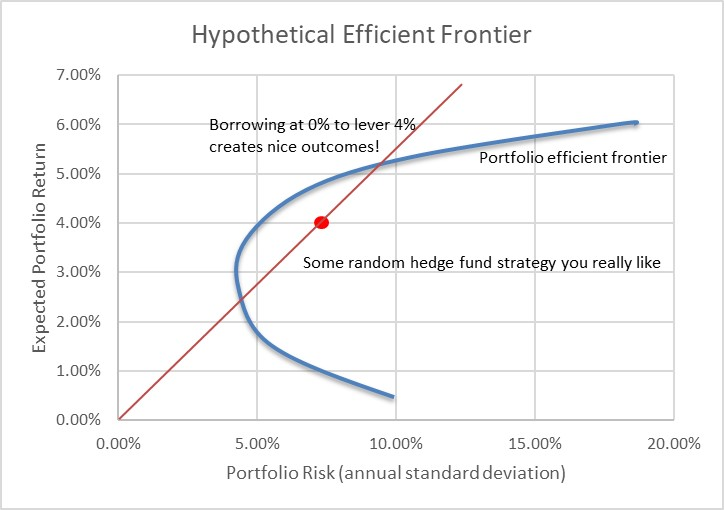Frontière efficiente hypothétique
Si vous pouvez emprunter à zéro, l’effet de levier multiplie simplement le risque et le rendement simultanément. Avec un effet de levier de 2 fois, votre rendement est de (2 x 4 % – 1 x 0 %) = 8 %. Vous pouvez voir où cela mène puisque 0 fois quoi que ce soit disparaît de la formule.
Mais cela ne fonctionne pas lorsque le coût de l’effet de levier est plus élevé. Si le coût de l’effet de levier est égal au rendement attendu, vous augmentez le risque à chaque fois que vous utilisez l’effet de levier. Et si le coût de l’effet de levier est supérieur au rendement attendu, vous aggravez la situation à chaque fois que vous ajoutez de l’effet de levier.
Frontière efficiente hypothétique
Il n’est donc pas judicieux d’utiliser des stratégies à faible rendement à moins que le coût de l’effet de levier ne soit très faible. De même, il n’est pas très judicieux d’exploiter des stratégies à haut rendement, à moins qu’elles ne présentent un faible risque. En effet, ces calculs ne s’appliquent pas uniquement aux rendements attendus, mais aussi (et surtout) aux rendements réels.
Supposons que vous ayez une stratégie dont le rendement attendu est de 6 % et le risque de 15 %. Il s’agit par exemple d’un indice d’actions. Vous le multipliez par deux, le coût de l’effet de levier étant de 5 % (d’ailleurs, si vous utilisez un ETF à effet de levier, vous n’échappez pas au coût de l’effet de levier… mais c’est pour un autre jour). Votre rendement attendu est maintenant de 7 %, avec un risque de 30 % (vérifiez votre compréhension en faisant le calcul).
Cependant, vous obtenez maintenant un résultat de 2 écarts-types à la baisse. En principe, cela ne se produit qu’une année sur 40, mais nous savons qu’il y a des queues de poisson dans les marchés d’actions. Quelle que soit la probabilité réelle, votre rendement sans effet de levier est désormais de 6 % – 2 x 15 % = -24 %. Mais maintenant, vous surfez sur l’éclair et votre rendement sur l’effet de levier de 2 fois est de (2 x -24 % – 5 %) = -53 %. (Sinon, vous obtenez le même chiffre si vous considérez simplement le nouveau rendement du portefeuille à 7 % de risque/30 % comme 7 % – 2 x 30 %).
Les gestionnaires de fonds spéculatifs comprennent ce calcul… ou devraient le comprendre ; s’ils ne le comprennent pas, qu’ils s’en aillent… et cela devrait modifier les chiffres qu’ils communiquent dans leurs déclarations prospectives lorsque les taux d’intérêt sont plus élevés, pour les stratégies à effet de levier. Je ne commenterai pas les pratiques normales du secteur…
*Pour être clair, aucun des points rouges de cet article ne représente le compromis risque/rendement de cette stratégie. Je n’essaie pas de présenter avec cagilité la performance de notre fonds, car cela m’attirerait des ennuis.
**C’était l’âge d’or du blog. À peu près au même moment, j’ai également publié l’un de mes meilleurs articles depuis des années, soulignant que la durée du contrat obligataire CME s’est raccourcie et que sa convexité est à nouveau négative. «Comment des taux plus élevés entraînent des changements importants dans le contrat obligataire». J’ai adoré cet article.
